Description

Daenerys Targaryen has an army consisting of $k$ groups of soldiers, the $i$-th group contains aisoldiers. She wants to bring her army to the other side of the sea to get the Iron Throne. She has recently bought an airplane to carry her army through the sea. The airplane has $n$ rows, each of them has $8$ seats. We call two seats neighbor, if they are in the same row and in seats {1, 2}, {3, 4}, {4, 5}, {5, 6} or {7, 8}.

A row in the airplane

Daenerys Targaryen wants to place her army in the plane so that there are no two soldiers from different groups sitting on neighboring seats.

Your task is to determine if there is a possible arranging of her army in the airplane such that the condition above is satisfied.

Format

Input

The input will consist of a series of test cases. Each test case consist of two line.

The first line contains two integers $n$ and $k$ $(1 \leq n \leq 10000, 1 \leq k \leq 100)$ — the number of rows and the number of groups of soldiers, respectively.

The second line contains k integers $a_1, a_2, a_3, \dots, a_k$ $(1 \leq a_i \leq 10000)$, where $a_i$ denotes the number of soldiers in the $i$-th group.

It is guaranteed that $a_1 + a_2 + \dots + a_k ≤ 8n$.

Output

If we can place the soldiers in the airplane print "$YES$" (without quotes). Otherwise print "$NO$" (without quotes).

Samples

2 2
5 8
1 2
7 1
1 2
4 4
1 4
2 2 1 2

YES
NO
YES
YES

#Hints In the first sample, Daenerys can place the soldiers like in the figure below:

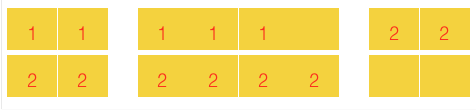
In the second sample, there is no way to place the soldiers in the plane since the second group soldier will always have a seat neighboring to someone from the first group.

In the third example Daenerys can place the first group on seats (1, 2, 7, 8), and the second group an all the remaining seats.

In the fourth example she can place the first two groups on seats (1, 2) and (7, 8), the third group on seats (3), and the fourth group on seats (5, 6).